
Example 1 for theEvaluation of Twice Exposed Picturesby means of simulated pictures of the 2004 transit of VenusU. Backhaus, University of Duisburg-EssenThis example demonstrates the procedure of measuring and evaluating of transit photos in order to determine the distance to the Sun. The procedure is described in detail and explained with an example in a basic paper. While going through this example, that paper should be present. Two "photos" are given which have been exposed twice with fixed camera simultaneously in Essen and Windhoek at 10.00 UT.


In order to derive the distance to the Sun from this pictures with the basic formaula 
In addition to the pictures, the following informations are given:
(There are additional projects concerning the determination of these quantities by means of own measurements!)
Evaluation
The relative distances ρ' between Venus and the centre of the solar disc and the corresponding position angles can be determined by means of the computer program Bildauswertung.
Results:
Results (They are given by the program, too.):
From these results, the parallactic shifts can be calculated as multiples of the solar radius:
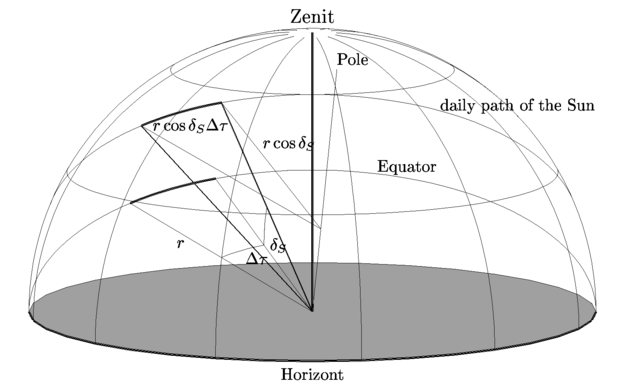
At the equinoxes, when the Sun's position is exact on the celestial equator, it moves by exact 360° in 24 hours. Its angular velocity, therefore, is ω0 = 360°/24h = 1°/4m = 15"/s. However, if it is distant from the equator by its declination δS, the radius of its daily path is smaller by the factor cosδS. Its angular velocity is then ω = ω0cosδS and, therefore, ω=13.82"/s on June 8th. On the photos, both pictures of the Sun are seperated by 279.3 pixels. During the corresponding time interval of 90s, the Sun has moved by 1243.8". Therefore, the scale of the pictures is 4.45"/pixels The solar radius on the pictures is 213 pixels. The angular radius of the Sun, therefore, is ρS=948.5"=15.81'. Therefore, we get the following parallactic shifts of Venus from the relative parallactic shift calculated above:

First, the polar geographical coordinates are transformed to rectangular coordinates. The Earth's centre is the origin of the corresponding system of coordinates and the equatorial plane its x-y-plane. The x-axis points to the longitude of Greenwich.
Thus, the linear distance between both sites is Δ/RE = 1.21. Remark: Because of the difficulty of the following calculation of the projection angle, it is worthwhile to calculate approximations for the solar parallax by the assumption that this angle is nearly 90°: |
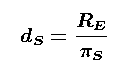


 Udo Backhaus
Udo Backhaus