 Essen, horizontal view
Essen, horizontal view
Internet Project
Observing, Photographing and Evaluating the
Transit of Venus, June 8th, 2004
 Essen, equatorial view
Essen, equatorial view
 Essen, horizontal view
Essen, horizontal view
|
Internet ProjectObserving, Photographing and Evaluating theTransit of Venus, June 8th, 2004 |
 Essen, equatorial view
Essen, equatorial view
|

The distance Δ can be calculated when the geographical coordinates of the both observers are known. For the calculation of w it is necessary to determine the local sideral time of the observers and the position of the Sun, that means its geocentric equatorial coordinates.
There are two tasks for measurements:
Because the geographical positions influence the result for the parallax of
the Sun only weakly quite rough methods of "astronomical navigation"
are sufficient.
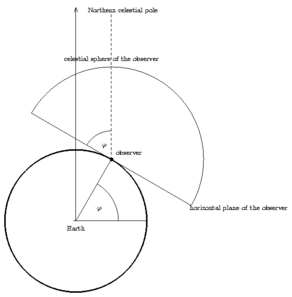
The geographical latitude equals the elevation of the northern celestial pole
and, with sufficient accuracy, that of Polar Star:
Unfortunately, there is no as simple method for observers on the southern
hemisphere! But it is possible to apply the method which is described for the
Sun, below, to a star with known declination.
The simplest method is to measure the elevation of the Sun at noon. The best
way to do that is described in project 3
where not the maximal elevation but the time of culmination is of interest.
Measurements of longitude are measurements of time! (A possible device is
pictured in project 4.)
If you know the local sideral time you can derive the longitude by the
following algorithm:
A more precise way is to measure the time of culmination of a star with known
right ascension:
To be able to recognize the time of culmination you should know the exact
direction to south.
In this case, you should measure the time of local midday, that is the time at
which the Sun culminates, by the method described in
project 3:
If you live east of Greenwich the Sun will culminate before 12.00 UT! For
exactness, this equation had to be corrected by the equation of time. But
because in June this correction would be small it has been omitted.
Your longitude, therefore, can be calculated in the following way:
To be able to calculate the angle of projection w you must know the
vector connecting two observers and the vector directing to the Sun in the
same coordinate system. As we already know the position of the Sun in
geocentric equatorial coordinates we want to transform the positions of the
observers in that system, too.
Pooh, a lot of work have been done. But now it is easy, at least in principle,
to calculate the angle of projection:
The rectangular positions are then given by:
Finally, we get the projection angle from the following equation:
1. The geographical position
For these measurements, it is suitable to have determined the exact
direction to south in advance (project
3)!
1.1 Geographical latitude
1.1.1 at night

1.1.2 during the daytime
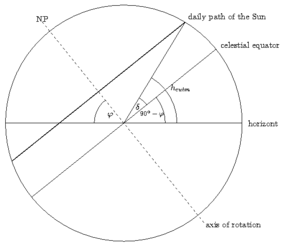
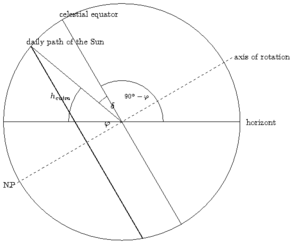
maximal elevation for northern sites
maximal elevation for southern sites


1.2 Geographical longitude
1.2.1 at night
The simplest way to determine local sideral time is to use the "celestial
clock":
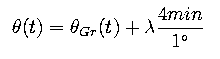


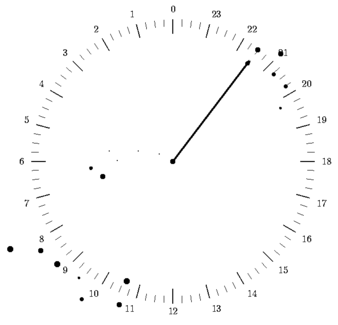
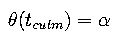
1.2.2 during the daytime


2. The position of the Sun
The position of the Sun ca be determined by the same procedures as described
above (Caution: There is a certain danger to get into a tautology!)


3. The angle of projection




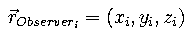





 Prof. Dr. Udo Backhaus
Prof. Dr. Udo Backhaus
last modification: March 28th, 2008