 Essen, horizontal view
Essen, horizontal view
|
Internet Project
Observing, Photographing and Evaluating the
Transit of Venus, June 8th, 2004
|
 Essen, equatorial view
Essen, equatorial view
|
Project 1: Measuring the Radius of Venus' Orbit
To be able to derive an own measure of the Astronomical Unit from the
self determined value of the Sun's parallax by the following equation (see the
related paper (in German or in English))
 you need to determine, among other quantities, the radius
rV of Venus' orbit or, to be more precise, the
relation rV /rE between the radii of the
orbits of Venus and the Earth.
you need to determine, among other quantities, the radius
rV of Venus' orbit or, to be more precise, the
relation rV /rE between the radii of the
orbits of Venus and the Earth.
There are several possibilities for this measurement:
- Measuring the maximum angular distance between Sun and Venus both of them
above the horizont at the same time by means of a simple device for angle
measurements or, alternatively, with a sextant.
- Other methods of determing the maximum angular distance between Sun and
Venus, for instance
- observing Venus at the night sky, recognizing her position relative to
stars in the neighborhood and determing her equatorial
position by drawing her into a star map and
- measuring the exact horizontal position of the Sun and transforming her
horizontal to equatorial coordinates. (For this method, you need to know how
to determine the local sideral time and your own
geographical position.)
- Observing Venus during her retrograde motion and measuring her
equatorial positon at least two times.
All of these methods make use of the following simplifications:
- All planets move in the same plane as the Earth.
- All orbits are circles with the Sun in their center.
- All planets move with constant speed.
1. Direct measurement of the maximum angular distance between Sun and
Venus
When the angular distance between Sun and Venus, observed from Earth, has its
maximum value the triangle Sun - Venus - Earth is rectangular.
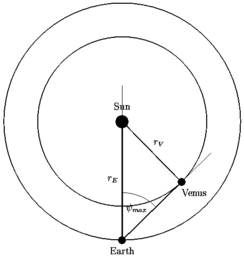 Therefore, the radius of Venus' orbit, in Astronomical Units, can easily be
determined by measuring the maximum angular distance between Sun and Venus:
Therefore, the radius of Venus' orbit, in Astronomical Units, can easily be
determined by measuring the maximum angular distance between Sun and Venus:
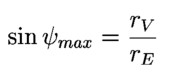
Because Venus will reach the maximum angular distance to the Sun around the
end of March 2004 the suitable time for doing these measurements are
the weeks of March and April 2004! In these weeks, Venus will play the role of
the evening star so that the measurements can be done in the evening.
The following possibility will occur after the transit in August. Than, Venus
will act as morning star.
The simplest method to measure the distance and to determine its maximum is to
observe both objects above the horizont, simultaneously. If you observe
Venus at the night sky early in the morning you will be able to find her
shortly after sunrise.

Proposals for rough measurements of the angle:
(You may get an impression of the measurements on our first result page.)
- Mark the lines of sight with pins on a piece of carton.
- Use a pair of compasses.
Perhaps you will find other simple possibilities.
A more precise method is to use a sextant a device which was invented just for
this kind of measurements.

2. Measuring the equatorial positions of Venus and the Sun
This method is more precise than that described above. But it is more
indirect and you need more knowledge (about celestial coordinates and sideral
time, for instance) and more mathematical abilities (transformation of
coordinates and so on).
2.1 Position of the Sun
The simplest method of measuring the equatorial position of the Sun is to
measure the exact time of its culmination and its maximum elevation. Then,
there holds a simple relation between declination of the Sun, geographical
latitude of the observer and the maximum elevation, for instance with a
gnomon (see also project 2):
 (for northern latitude)
(for northern latitude)
 (for southern latitude)
(for southern latitude)
The right ascension of the Sun is just the exact local sideral time of the
time of culmination.
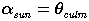
2.2 Position of Venus
The easiest method of determing the celestial position of Venus is to observe
her exact position among the stars before sunrise and draw her into a sky map
from which you can read the equatorial coordinates.

Position of Venus and Mars on January 11th, 2003
2.3 Evaluating the horizontal position of Venus and Sun
For this method you have to measure the azimut A, for instance
with a magnetic compass, and the elevation h above the
horizont and the exact time of your measurement. From this values, you can
derive the equatorial coordinates by the following algorithm:
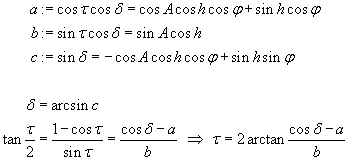
From the hour angle, you can derive the right ascension when you know the
local sideral time:
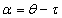
2.4 Calculating the angular distance
If you know the equatorial positions of Venus and the Sun it is not difficult
to calculate their angular distance by the following formular (see below):
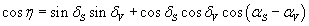
3. Observing Venus during her retrograde motion
This method can be applied only in a short time interval around the transit,
that is between May 23th and June 28th!

Venus' positions at the beginning and at the end of its retrograde motion
Around the inferior conjunction of Venus, at the sky the planet will move
retrogradely that means opposite to its usual direction (from east to west).
That's why Venus overtakes the Earth in that time. The picture below gives an
explanation for this fact not only in a qualitative way but in a quantitative,
too.
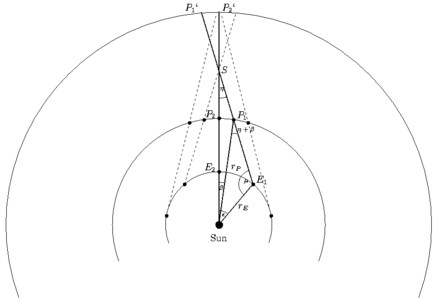
Explanation of the retrograde motion of a superior planet. In the case of
Venus which is an inferior planet you must change the letters P and
E. The argumentation remains unaltered.
In the triangle Sun - E1 - P1, the
following equation holds:

Looking at the triangle Sun - E1 - S you may
realize the following identity:
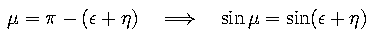
Combining the both equations, we get the following result:

We hope that we will be able to observe and to measure Venus's position in its
inferior conjunction, that is during its transit! Thus, we can measure its
right ascension and declination on that day (see project 4). If we will be able to measure Venus'
position on an additional day during its retrograde motion we can determine
the anglular distance η between these both positions by the
following relation:


The central angles at the Sun can be derived from the mean daily motion of
the planets which are due to their sideral periods:

Generalization
If we will be unlucky and not able to observe the transit we, nevertheless,
can apply the above method by measuring Venus' position during its retrograde
motion twice. In this case, the following equation must hold:
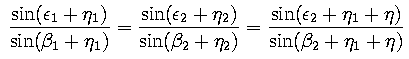
In this equation, the single angles η1 and
η2 are unknown. Only the angle
η=η2-η1 has been measured. The
central angles are again determined with respect to the date of conjunction.
The following function f must, therefore, be zero at the
point η1:
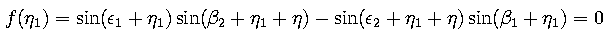
This is a well known numerical problem and can be solved by trial and
error, by a graphical method or by a numerical algorithm, respectively. You
may download a little program which does the
work for you.
4. First Results
Groups in Fürstenwalde und Essen have determined the radius of Venus'
orbit between the end of December 2002 and the end of January 2003. The
results are shortly combined in a result page.
The mean value of these measurements is:
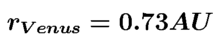
back to the main page


 Prof. Dr. Udo Backhaus
Prof. Dr. Udo Backhaus
last modification: March 28th, 2008
 Essen, horizontal view
Essen, horizontal view
 Essen, equatorial view
Essen, equatorial view
 Essen, horizontal view
Essen, horizontal view
 Essen, equatorial view
Essen, equatorial view


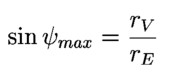


 (for northern latitude)
(for northern latitude)
 (for southern latitude)
(for southern latitude)
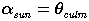

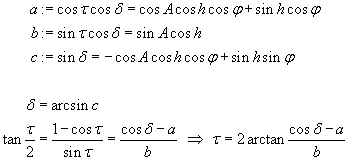
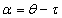
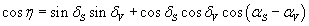



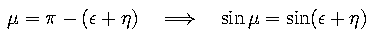




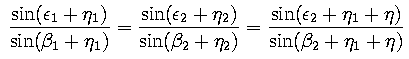
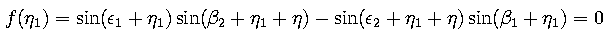
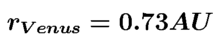


 Prof. Dr. Udo Backhaus
Prof. Dr. Udo Backhaus